Abstract

This ML model allows us to understand the relationship between our marketing media investments with the impact/sales generated. The model tries to learn the different effects that make up our sales and gains insights on how we are investing into the different media ad platforms and how much impact we receive from it. We further learn the saturation curves to each of these vehicles, for every week and brand, which is furthered used to run optimization scenarios to find most optimal allocation of our budget on each brand, media vehicle and week.

Problem Statement

We need to create a Mixed Marketing ML Model (MMM) that learns to estimate the impact of various marketing investments, made by ABI on their different variety of brands on every country, on sales and forecast the impact of future investments.

Further, based on the MMM ML model learns, we need to run optimization on the saturation curves predicted by the model to allocate budgets effectively.

Solution

MMM ML Model

The MMM ML model learns how your impacts are decomposed based on the different effects and investments made on your marketing vehicles. When we invest $1,000 on a given vehicle, the sales we receive are not just generated from the $1,000 investment we made but rather also from different effects that took place, like holiday, weather, promotions, inflation, region, population, etc. If we can split our impacts into these different factors, we will be able to identify how much exactly the incremental impact was generated by spending on the given marketing vehicle. This helps us identify if the marketing vehicle is indeed effective or not and how much is recommended to spend on it? We learn 2 things the ROI curves and the Historical Decomposition of vehicles and its investments.

Historical Decomposition

The historical decomposition is capable in learning how the different sales generated over time is broken down into the different effects that has taken place. Temperature is an effect that takes place which impacts how we drink and consume ABI products. When the temperature rises there is a positive impact on sales. When there is inflation or unemployment in the region, this contributes to a negative impact on sales. Let's say if we did not make any investments in marketing and didn't have any significant effects happening, we would still be able to sell products without any of this, this is our baseline where these effects gets applied on. The remaining is the incremental impact that investing on the marketing vehicle made!

This gives us an intuition on why the products are sold and how much of an impact does spending on a vehicle gives us? This is gives us the decomposition of sales over time and is useful for us to forecast and later generate the ROI curves for each marketing vehicle to find the model optimal sales.

ROI Curves

The ROI curves are generated after learning the historical decomposition. These graphs constitute of 2 axis, the x axis which is the different spends laid out in a geometric series, the y axis is the incremental impact/volume that can be sold for the given spend amount. This is a saturating curve that is in the shape of a sigmoid curve

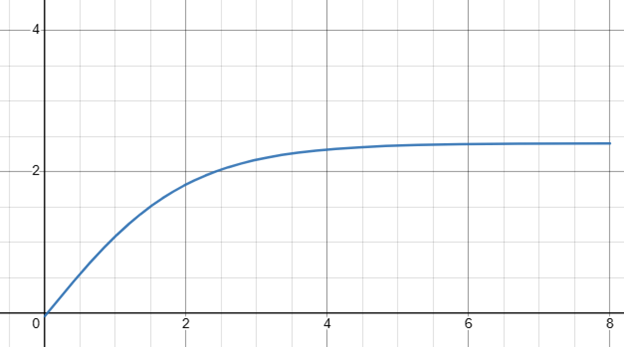
As you can see from the graph, the marketing vehicle saturates after a certain point and we need to invest in the more profitable range.

The ROI curves are generated for a country, brand, marketing vehicle and time (weekly), and they will have different saturation points. These ROI curves are further used for optimization to find the model optimal allocation. Note that these curves are convex in nature.

Budget Allocation

The ROI curves are used as inputs here, we take user inputs like marketing budget, the marketing vehicles we will be using to invest, and the brands that will make use of this marketing budget, the user level constraints like contracts which suggests the min and max allowed amounts for different brand, vehicle time combinations. We take all of these inputs and perform convex optimization to find the most optimal allocation of our marketing budget to different brands, marketing vehicles and time in order to get the highest/optimal ROI. Since the curves are convex in nature, it is mathematically given that there is only 1 single optimal allocation for the given input.

The objective function we are trying to maximize is

\[ \max_{x} f(x) = \sum_{b,v,t=0}^{\text{num\_brands,\ num\_vehicles,\ weeks}} \bigg(\frac{\text{impacts}_{b,v,t}}{\text{allocated investment}_{b,v,t}}\bigg) \]

Ideal Budget

What is the maximum budget that we can have for the given ROI curve, constraints, etc. after which we start to lose money? This gives us insight into what is the maximum amount that we are allowed to spend to get the highest profit but not necessarily the best ROI. This useful in finding out how much maximum budget we would like to assign to certain brand vehicle etc. to do better planning in the future.

The objective function we are trying to maximize is

\[ maximize\ f(x) = \sum_{\forall \ b,v,t} \ (net\ revenue_{b,v,t} - allocated \ investment_{ b,v,t} ) \]